The use of encrypted traffic on the Internet has become increasingly popular in recent years. Google and the Mozilla Foundation have released statistical data indicating that more than half of their browser users used HTTPS protocol-encrypted connections in 2016. Encrypted network traffic may conceal malicious software connections and hacker attack activities. According to Cisco’s reports, malicious software that communicates via TLS-encrypted connections accounted for 2.21% in 2015, whereas that figure increased to 21.44% in May 2017. Malicious software even uses Darknet and VPNs to connect with command and control servers. NSS Labs estimated that 3/4 of all network traffic will use encryption in 2019. Therefore, when the entire Internet embraces the benefits of encrypted connections, those who engage in sabotage, malicious software, and cyber intrusions will also be protected by this mechanism. In this article, we present a technique that utilizes a machine learning approach to identify malicious activity in encrypted traffic. We hope that this solution can be used to effectively control network traffic. In the following section, we will briefly describe the feature extraction of the encrypted traffic.
Feature extraction
A. Connection Records: Internet protocols and connection statistics [1] are significant in the identification of Internet traffic flow. Thus, we extract connection records, including the port, IP, and protocol information of the transport layer. In addition, according to Anderson et al. [2] and Tseng et al. [3], the information regarding HTTP requests and TLS handshakes also plays a crucial role in traffic identification. This information can be obtained from TCP payloads.
B. Network Packet Payload: TCP payloads occasionally send encrypted information under TLS or SSL protocols. To trace malicious flows and accompanying malware, the transmitted data of all TCP or UDP payloads should be considered. Hence, we extract all payloads from each packet, where the length of each packet ranges from 0 to 1,500 bytes.
C. Flow Behavior: Flow behavior can be used to monitor the sending process of packets; however, each malware family possesses different characteristics of flow behavior. Moore et al. [4] proposed nearly 250 discriminators to classify the flow record. Among these discriminators, the inter-arrival time of each packet within a flow plays the most important role in traffic classification. In addition, McGrew et al. [5] used a Markov matrix to store the relationship between sequential packets. Inspired by their methods, we utilize a Markov transition matrix to represent the flow behavior and record the before-and-after relationship.
We apply the above feature selections to several malicious data flows collected through a self-built sandbox. In addition, VPN/Non-VPN and Tor-NonTor datasets were requested from the Canadian Institute for Cybersecurity of UNB University. In the following section, we use the deep learning approach with the proposed learning algorithm (QPBP) to solve the imbalanced dataset problem.
Deep learning methodology
In this section, the proposed algorithm devised to solve gradient dilution due to the imbalanced data problem is introduced.
A. Quantity-Dependent Backpropagation (QDBP)
Backpropagation is a gradient-based method to train neural networks. The mathematical formula is given by:
where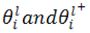 
represent the 
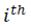parameter in layer l and the updated parameter, respectively, η is the learning rate, and 
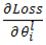refers to the partial derivative of loss with respect to 
.
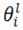However, neither the backpropagation nor adaptive learning rate approach can reflect the sensitivity toward minority classes, whether applying online learning or the batch learning mechanism, since both methods treat each class evenly. When imbalanced data distribution occurs, these methods will cause the model to have difficulty learning from the minority classes due to the gradient dilution issue. To mitigate this issue, we introduce a vector F into the backpropagation (equation (1)) and propose the QDBP algorithm, which considered the disparity between classes. The mathematical formula is given by the following equations:
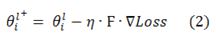
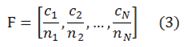
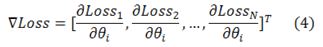
where F is a row vector, N represents the cardinality of the training dataset,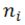 
represents the cardinality of the class to which the 
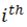datum belongs, and 
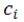is the pre-selected coefficient for the class to which the 
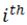datum belongs. The adjustment of 
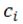depends on the sensitivity of the model to the gradients contributed by the data belonging to class 
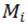. ∇Loss is a column vector composed of the partial derivatives of loss with respect to θ contributed by each datum. For example, if the 
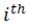datum belongs to class 
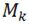, and the pre-selected coefficient for class 
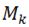is c, then 
= |
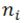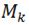|, and 
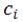= c. From equation (2), we can show that:
where M represents the training dataset,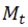 
refers to the 
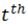class in M, and 
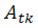is the 
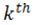datum of 
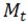. By setting 
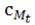to 1, ∀
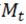∈ M
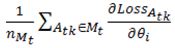can be viewed as the normalized equivalent gradient computed by each datum 
, ∀ 
∈ 
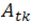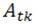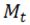since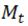 
= | 
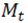|. Under this mechanism, the gradient dilution issue will be mitigated since the total gradient contributed by each class accounts for the same proportion. In our experiments, to reflect the sensitivity of the minority class, the pre-selected coefficient for the minority class is set to 1.2, while the other coefficients remain at 1.
B. Tree-Shaped Deep Neural Network (TSDNN)
To solve the problem of imbalanced data, we propose an end-to-end TSDNN model. The three-tier architecture of the model is shown in Fig. 1. The conventional multilayer neural network architecture is a static structure, whereas our architecture can be dynamically adjusted and extended. Similar to the first-level architecture in the figure, we can first divide the network traffic into two types: good and bad. Entering the second-tier architecture, the data are then divided into five different attack types. At the last level, we further classify the specific attack type into different families. The TSDNN can also use the QDBP method mentioned earlier to increase training effectiveness. The advantage is that dynamic adjustments of the proposed architecture can be made to accommodate a new type of attack mode more efficiently.
Experiments
Our previous results [3] could achieve 93% accuracy in malicious flow detection using only HTTP headers and TCP payloads. After including the new features mentioned in the previous section, we can achieve an accuracy of 99% under vanilla backpropagation. If we further apply QDBP, the recognition rate can improve further to 99.7%. This result shows that the additional features contribute to performance improvement.
We also compare the result with the state-of-the-art methods [6], [7], [8]. As illustrated in Table 1, the performance of the vanilla backpropagation is seriously affected by the gradient dilution issue because the cardinality of the “Bot” and “Cryptomix” classes is considerably smaller than that of the “Benign” class. Although the state-of-the-art methods can improve the classification performance, these methods still cannot resolve the gradient dilution issue. If the proposed TSDNN is trained with QDBP, the recognition rate can achieve an accuracy of 99.63% and a precision of 85.4%, outperforming the other approaches.
There are various kinds of malware in cyber society. However, data samples of each family cannot be collected, as there are many new variants of malware every day. To evaluate the generalization performance of the proposed model, we wanted to examine the ability of the TSDNN to identify some malware that has never been trained by our model. This kind of scenario is coined as “zeroshot learning” in machine learning terms. Therefore, we collected 14 different kinds of malware (Fig. 2) to evaluate the performance. The experimental results are shown in Fig. 2. The experimental results illustrate that our model performs reasonably well in recognizing this malware. In the real world, each attack usually has several network flows. Once any part of these flows is recognized as a malicious connection, the attack will be blocked, and the malicious communication process will be terminated immediately. This result not only demonstrates the ability to predict potential threats but further justifies that a behavior-oriented approach to detect malware is superior to conventional signature-based methods.
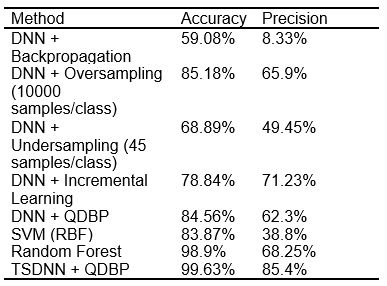
Table 1. Accuracy and precision of different approaches
Figure 1. This model performs 12-class classification in three stages. First, the model performs a coarse classification that preliminarily classifies the data into the class of benign flows and malicious flows. Second, the model conducts a multi-class classification on the malicious flows, which classifies them into 5 different categories according to the attack behavior. Finally, the model executes a fine-grained classification on the ransomware family.
Figure 2. The new malware dataset contains 14 different families, which are different from those used to train the TSDNN.
References
1. Williams, N., Zander, S., and Armitage, G. (2006). A preliminary performance comparison of five machine learning algorithms for practical IP traffic flow classification. ACM SIGCOMM Computer Communication Review, 36(5), 5-16. DOI:10.1145/1163593.1163596
2. Anderson, B., Paul, S., and Mcgrew, D. (2016). Deciphering malware’s use of TLS (without decryption). arXiv preprint, arXiv:1607.01639 [cs.CR].
3. Tseng, A., Chen, Y., Kao, Y., and Lin, T. (2016). Deep learning for ransomware detection. IEICE Technical Report, 116(282), Paper #IA2016-46, 87-92.
4. Moore, A., Zuev, D., and Crogan, M. (2013). Discriminators for use in flow-based classification. Technical Report for Intel Research, Cambridge.
5. McGrew, D., and Anderson, B. (2016). Enhanced telemetry for encrypted threat analytics. In IEEE 24th International Conference on Network Protocols (ICNP), 1-6.
6. Pears, R., Finlay, J., and Connor, A. M. (2014). Synthetic minority over-sampling technique (smote) for predicting software build outcomes. arXiv preprint arXiv:1407.2330 [cs.SE].
7. Liu, X., Wu, J., and Zhou, Z. (2009). Exploratory undersampling for class-imbalance learning. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 39(2), 539-550.
8. Kulkarni, P., & Ade, R. (2014). Incremental learning from unbalanced data with concept class, concept drift and missing features: a Review. International Journal of Data Mining & Knowledge Management Process, 4(6), 15-29. DOI:10.5121/ijdkp.2014.4602
Tsungnan Lin
Professor, Graduate Institute of Communication Engineering